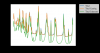
I using Levin's method (Internal thermal noise in the LIGO test masses: A direct approach) of using the suceptability of a mirror to a force resembling the laser beam profile to model the thermal noise, I modeled the GQuEST end mirrors as 2 mm thick, 1 in side length squares made of silicon with a Q of 10^6. I added a coating 20 um thick made of silicon as well but with a Q of 10^3. I constrained the 4 side of the mirror to only move in the z-axis. The spot radius is 2 mm. The face of the mirror had 52 x 52 mesh points, the substrate had 10 layers of mesh, and the coating had 3 layers of mesh. I simulated from 500 kHz to 16.5 MHz with 100 kHz frequency spacing. It look 5 hours and 17 minutes. Attached is the data converted into an ASD. The coating thermal noise, due to its low Q and that the force is applied on it, dominates the "bottom of the bucket".
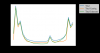
I repeated the simulation but with a loss angle of 1e-4 instead of 1e-3 for the coating, no clamping of any kind, and a mesh 2x as dense in all 3 axes. The coating thermal noise does not fall off as hypothesized.
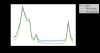
I repeated the most recent simulation but made the mesh 3x more coarse in all 3 axes. The amplitudes between the peaks is very similar. Interestingly, the frequencies of the peaks are changed compared to the fine mesh.
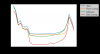
I added a back coating to the mirror. The loss angle for the coatings is 1e-4 and there is no clamping, but otherwise this simulation is identical to the original simulation.