In order to see whether some of the resonances in the output filter cavities are due to a mechanical self resonance in the long axis, here is a simple calculation to see whether it's possible:

\[\omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{EA/L}{\rho AL}} = \frac{1}{L} \sqrt{\frac{E}{\rho}} \]

\[f = \frac{\omega}{2\pi} = \frac{1}{2\pi L} \sqrt{\frac{E}{\rho}} = \frac{1}{2\pi \ 0.5 m} \sqrt{\frac{69 GPa}{2700 kg/m^3}} = 1600 Hz\]

Here, \omega is the angular frequency, k is the spring constant, m is the mass, E is Young's modulus, A is the cross sectional area, L is the length, \rho is the density, and f is the frequency.

It appears that the worst resonances in the cavity spectra are closer to 4 kHz, so either this is too simple a model or that resonance is due to something else.

[Ian, Torrey, Daniel]

We moved the 2 end cubes (not bend cubes) from B150 to B102. Since the end cubes bases have screws sticking out, they are resting on my custom base plates flipped upsidedown. The next steps are to take the bottoms off, put on my custom base, clean the insides, and move them to their final location. We will then start assembling the rest of the vacuum equipment for the LFC.

[Lee, Daniel]

Lee has updated the model of bulk acoustic wave noise in GWINC (I believe to account more accurately for shear modes), but the results seem to indicate more bulk acoustic wave noise than the Holometer measured or I have modeled with COMSOL. Attached are 4 figures. The first is the measured Holometer data (fig 12.) The second is a plot from the GWINC model of the Holometer. The differences between the GQuEST model and Holometer model are arm length, laser wavelength, arm power, mirror size, mirror material, and mirror spot size. The Holometer end mirrors were modeled as 0.5" thick, 1" radius and the beamsplitter as 0.5" thick, 1.5" radius. Both were made from fused silica at 294 K. The beam size on the end mirrors is 5 mm. The calculated noise in GWINC is a maybe bit higher in this model, but it is fairly close.

I also did 2 COMSOL simulations with a 2 mm thick, 12 mm side length mirror with a beam waist of 2 mm with 1e6 Q Silicon. Both simulations had 14 mesh layers in the beam axis. For the first simulation, there were 42 mesh layers on each transverse side. For the second simulation, there were 84 mesh layers on each transverse side (making the mesh elements cubes). The minimum value of the graphs is nearly identical. Comparing the peaks is less meaningful because of aliasing due to the course frequency sampling of 100 kHz. The fact that the minima are so close implies that previous COMSOL simulations, which showed minimal noise from shear modes outside of certain peaks, were not limited by the transverse mesh density. Lee points out that the Krylov-space inversion solver might drop modes since it is a reduced-order solver. I am therefore running an eigenmode solver right now.

[Torrey, Ian, Daniel, Sander, Lee]

Introduction

We have been struggling for a while to figure out a configuration for a stable cavity lock using only the piezo mirrors. In an effort to troubleshoot, we want to take a transfer function of just the piezo (h_p). We can't do this directly while the cavity is aligned and locked so we have to be a little clever about it. Below is a how we go about doing this.

Set up and methods

In the moku multi-instrument mode we can set up a combination of transfer functions to achieve the piezo transfer function. As seen in this, we lock the cavity with the laser. The digital filter box is used as a summer. Output 1 is used to control the DC modulation port of the ULN15TK laser and Output 2 is used for the cavity piezo. Output 3 is the 50 MHz signal used for demod. Input 1 is the newport 1811 high bandwidth PD in reflection of the cavity. Input 2 is the GE lower bandwidth PD in transmission of the cavity. Two transfer functions are set up in this configuration:

1. Fast controller (laser frequency controller) divided by excitation to laser frequency.
2. Fast controller (laser frequency controller) divided by excitation to the laser piezo.

We can reduce this diagram to a clearer picture of the control systems in play using a Signal Flow Graph (alternate picture to the more common block diagrams). This reduction can be seen as signal_flow.pdf. From this diagram we can see the open loop gain G can be written as \[G = H_1*F*H_2*\alpha.\] We can subsequently reduce our individual transfer functions into smaller diagrams, seen in reduction_A.pdf and reduction_B.pdf. From these it is a little easier to write down the equations for our transfer functions in terms of G and individual components. From reduction_A.pdf we see that,

\[T_p = V_{LF} \] and \[V_{VL} =  A + G V_{LF}.\] This means \[\frac{T_p}{A} = \frac{1}{1-G}.\] For now we will call this measurement one, or \[M_1 = \frac{T_p}{A} = \frac{1}{1-G}.\] Similarly from reduction_B.pdf,

\[T_p = \frac{H_p}{H_2} \frac{G}{1-G} B.\] Again lets call this measurement two, so \[M_2 = \frac{T_p}{B} = \frac{H_p}{H_2} \frac{G}{1-G}.\]

Take the ratio of M2 and M1:

\[\frac{M_2}{M_1} = G \frac{H_P}{H_2}\]. Substitute the above expression for G and solve for H₂,

\[H_p = \frac{M_2}{M_1} * \frac{1}{H_1 F \alpha}\].

This is a nice form as every variable can be obtained experimentally or is known already.

1. M1 and M2 are our measured transfered functions.
2. F is the filter used in the digital filter box which at the time of measurement 0 db for all frequencies so trivially F=1.
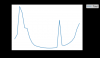
3. H_1 is the shape of the fast controller of the laser lock box. This is slightly annoying to recreate as there is no way to download the shape of the loop directly from the fast controller of the laser lock box. I get around this by recreating it in python using scipy. Most scipy functions seem to want the order of the filter and cutoff frequency; cutoff frequency being a problem as the controller shape is defined by the UGF and not cutoff frequency (ex: fast_controller_example.png). A conversion can be made but slightly annoying. Jeff is currently very close to being done with a script that will take these 6 inputs and recreate the shape of the controller in python.
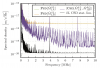
4. Alpha is the conversion from Hz into Volts from the laser frequency to the PDH lock. This is found by the ratio of the amplitude of the error signal in the PDH lock and the cavity bandwidth. The error_signal amplitude can be found trivially by putting one of the moku test points at the error signal. The cavity bandwidth can be derived or measured in a few different ways. The method we went with was to scan the laser frequency to see 0,0 peaks in the TRANS PD. This peak will have some width, from which the FWHM in time (delta t). In order to convert this to a frequency we do the following conversion:

\[\mathrm{BW(Hz)}  = \Delta t * \frac{2 A}{T} * \frac{2 mA}{V} \frac{5 pm}{20 mA} \frac{c}{\lambda^2}\]

• 2A/T converts the width of the peak from time to volts.
• 2 mA}/V is the conversion of the DC modulation quoted on the thorlabs website from input voltage to pump current modulation. 
• 5 pm/20 mA is how much the laser wavelength changes given some amount of change in pump current. Note that this is only true in the linear regime and is not true everywhere. For small changes, as is the case here, it is true.
• c/\lambda^2is the derivative df/d lambda of f=c/lambda to convert from meters to frequency.

From the data collected this yields approximately 307 kHz bandwidth for the cavity with the low reflectivity mirrors (R ~~ 99%).

Results

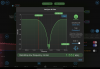
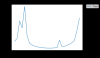
The final result of \[H_p = \frac{M_2}{M_1} * \frac{1}{H_1 F \alpha}\] yields result.png. I think there is a scaling factor off somewhere but the shape makes sense. Also something to look into is the low quality of the data at low frequencies, of which Lee has given me ideas on how to correct this. We cannot simply drive these things harder.

1) The LaserLockBox instrument is currently not fully configurable in Multi-Instument mode, the API does not allow you to configure the modulation output.  LaserLockBox in MultiInstrument

2) If you set filters with the API and then connect to the Moku via iPad, it resets the filters to default. Switching from API to GUI

I tried to remove the residue on the end cubes that was left over from the tape. I used isopropanol last week and acetone this week, but neither worked. I therefore covered the residue in Kapton so that the residue does not contaminate the lab space. See attached photo.

I removed the 2" long, 5/16-24 set screws from the 10" to 8" Flange Size Zero Length Reducer. The set screws do not have a hex drive (perhaps they are more accurately called studs), and ~16 of the 20 required pliers to remove. This caused a bit of silver plating to come off, but it was easily removed with an air duster. The ends of the screws furthest away from the flange were quite dirty and/or lost their silver coating. See attached photo.

I then used isopropanol and Kim wipes to clean the non vacuum part of the reducer. Some gunk made it into the part where the copper gasket lies outside the knife edge. I cleaned this to the best of my abilities. See attached photo.

[Alex]

In the netork settings page I have set the static IPv4 addresses for the Moku Pros and the Siglent SDS2104X HD Oscillascope.

See image bellow for their settings, but the curernt IP addresses were used to store as their static IP's.

To do this for another device, navigate to the network page at: http://192.168.50.1/ and login.

To set a new static IP:

     Navigate to the LAN sidebar tab under advanced settings.

     At the top, go to the DHCP Server tab, and at the bottom you will see a table labled: "Manually Assigned IP around the DHCP list (Max Limit : 64)"

    Set a new static IP by adding the Mac address of the device, the IP you wish to set, leave DNS servers blank, and put a descriptor of the device under Host Name.

To see a list of all network attached devices:

     Navigate to the Network Map sidebar tab.

     You will see a network flow chart and in the bottom left box under Clients click on "View List"

For more help come ask Alex or Ian.

I made and cleaned a "U Holder" to independently individual bowtie subassemblies like the piezo assembly. This U Holder has a counterbored hole for a #8 screw to go into a post or pedestal. Screwing into a 1 inch or 1.5 inch diameter pedestal requires a 0.5 in diameter spacer, which I have ordered from Newport. The height from the mounting point of the U holder to the center of the mirror is 1 inch.

After cleaning, I did a fit check, and the piezo assembly base screws into the U Holder.

I 3D printed a holder to hold the fiber for the FPC562 fiber paddle controller to change the polarization of the light in the fiber.

So that optics aren't damaged during assembly, I built an area designated for putting together optics and mounts. The area is covered in teflon to reduce damage if a drop does occur and has a 3D printed PLA ring to keep objects inside the square. Especially for BS cubes, the post should be forked down and the mount should be screwed into the mount. See attached photo.

I 3D printed a holder for the Covesion SHG and its fibers. 

Attached are descriptions of the measurement setup used in log post 11449, as well as transfer function and noise data.

The piezo used here was Thorlabs, as described in 11449. The piezo transfer functions taken in log post 11373 were of the Noliac, would it be useful to take the same measurement of the Thorlabs piezo? Should it give us the same transfer function we will get by quotienting the open loop transfer function by the controller?

The noise measurements were taken with the laser locked, with the fan off and fan on.

I 3D printed two aligment tools that slide into the corners of the bowtie cavity. The beam should pass through all 4 holes. The diameters are tight, so probably not the best to use for lining up the reflected beam and instead just use for the incident beam.

I 3D Printed a Basler ace 3 GigE Camera Mount. It sets the center of the camera 1 inch above the bottom of the mount.

I 3D printed an aligment tool that goes inside the bowtie cavities to aid alignment. The beam is suppose to go through the two holes. The hole diameter is 0.25 in so the beam shouldn't clip, although we should probably remove this during actual operation since there are other sites in which the beam almost clips.

I 3D printed a holder for the Beckman Coulter HHPC 3+ particle counter so that it can charge and be run simultaneously. This holder screws into the particle counter and into the optics table so that it doesn't tip over. There is also a taller prototype version which doesn't screw into the table in case wires that plug into the particle counter are too tall and stiff.

Torrey and Daniel October 3, 2023

Daniel 3D printed a cover for the ULN15TK Seeder Laser that makes it very difficult to accidentally turn on or off the seeder. Torrey printed and attached warning labels conveying that one should not turn the seeder off so that the amplifier isn't damaged. If we are really paranoid, Daniel could 3D print a cover with a tighter fit.