Correcting the Flat FOM gain to always be 1

[Ian, Lee]

NOTE: this should have been posted on June 21 2023 as this is the date that it was writen, but it was in my drafts for some reason. I have added latex since then

In the H2 system the gain for the flat FOM (F2) is 1/F1_gain, where F1_gain is the gain of the BNS FOM (F1). This works fine for the H2 norm because that is made up of the composite RMS from both FOMs so as one FOM's gain increases and the others decreases they cancel out. However, this is not the case in the H_infinity case. The H_infinity norm is the maximum value for the frequency response from the Zinf input to the Flat FOM output this value must be less than or equal to the gamma that we are using. Currently we are searching for a gamma around 1. The equation for the frequency response along the  Zinf input to the Flat FOM output is:

\[ \left | \frac{K(\omega)P(\omega)}{1-K(\omega)P(\omega)} F_{\text{flat}}(\omega)\right |\leq \gamma \]

where \( K(\omega)\) is the controller response, \(P(\omega)\) is the plant response and \(F_{\text{flat}}(\omega)\) is the Flat FOM's response. If the environmental noise is large like at low frequencies then \( K(\omega)P(\omega) \) must be large to control it. Thus at low frequencies the above equation becomes,

\[ \lim_{KP \to \infty }\left | \frac{K(\omega)P(\omega)}{1-K(\omega)P(\omega)} F_{\text{flat}}(\omega)\right | \approx\left |F_{\text{flat}}\right | \leq \gamma \]

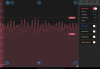
Thus if we use the F2_gain=1/F1_gain then as F1_gain gets very small F2_gain gets very large. When F2_gain is very large, the gamma we are searching for (around 1) is much less than the actual H_infinty norm which is on the order of the F2_gain and the solver fails. This is what was causing the problems with the RMS plot. 

We switched the F2 gain to be all ones and acquired attached plot.

Note: when this PDF is printed the second color bar has the same colors as the first color bar.

---

Improvements for code and plots for paper:

1. Fix the color bar problem (noted above) for printing.
2. Make the color bar discreet
3. decrease the number of F1_gain points so that the plot is not so crowded 
4. Maybe add an H2 boundary line. See how it looks
5. change the F1_gain color bar. maybe connect like F1_gain points with a subtle line.
6. Add an example of the model maker (getSPOFF) to Buzz
7. make the code transpose the model right before solving in the H_infinity case

GQuEST in One Page

Here is a one-page summary of GQuEST. Let's discuss!

Bowtie Cavity Mechanical Assembly

I added helicoils to a bowtie cavity, the piezo bases, and the mirror deformation bases. I also tapped the piezo bases and the mirror deformation bases with SM1 threads. I fully assembled a bowtie cavity as a fit check. Future steps: Add helicoils to the remaining bowtie cavities. Test the static mirror deformation. Purchasing required for bowtie cavities: Indium wire/foil 1 in Mirrors Piezos are currently being shipped 06/06/2023 Added helicoils to remaining bowtie cavities For some reason, one of the piezo bases had 3 through holes with too small a diameter. I reached out to Hubs to get a refund on that part. I can drill out the holes by ~4 thou so that the screws fit. Other than this issue, I was able to successfully fit check everything. I also successfully stacked two bowties on top of each other.

Holometer Disassembly June 20-June 23

While at Fermilab, I disassembled a lot of parts like the central vessels, two end cubes, and a lot of gate values and bellows. I specifically prepared two central vessels and two end cubes to be shipped by emptying their contents and covering the open ports with plastic and duct tape. There are also a lot of other parts nearly ready to be shipped, like 1 foot T pipes, that will be useful for the 0.5 m interferometer. Two (b)end cubes in the shed also need to be disassembled. We will probably need a lot of small parts. The only expensive part we need, as far as I can tell, is another end cube. The remaining two cubes are being used by other experiments. Remaining work: Get central vessels (2) and end cubes (2) out of building Disassemble (b)end cubes (2) Track down remaining end cube Prepare various pipe lengths to be shipped Prepare 8 inch gate valves (4?) to be shipped Prepare bellows to be shipped Have carpenters build structure to protect everything in shipping

Table Leveling and Condition

[Ian, Torrey]

The long table on the North wall of the transition lab was leveled by putting shims under the table legs (See Table_Before_Shims.jpeg). We found that there are adjustable feet under the legs and we extended them (See Table_After.jpeg).

While extending the legs we found that the table top was not attached to the frame of the table and almost impossible to level. We tried to level it the best we could but the table in general doesnt look to be in great shape.

Implementation of Balancing in State-Space Systems

[Ian, Lee]

Balancing state space systems is essential for getting the RMS plots correct for the comparison of controllers. When using the solution for the Lyapunov equation the solver benefits greatly. Adding the wrapped version of Slycot's AB09ND was the key to getting the H2 Lyapunov solver to correctly display the shape of the RMS H2 optimal curve. AB09ND "compute[s] a reduced order model (Ar,Br,Cr,Dr) for an original state-space representation (A,B,C,D) by using either the square-root or the balancing-free square-root Singular Perturbation Approximation (SPA) model reduction method for the ALPHA-stable part of the system" (from documentation).

Another way that was shown to be effective at helping the Laub method to work in some updates for GWINC is the TB01ID. We were wondering if this would be as effective on our code given that AB09ND is calling TB01ID. We ran the code with balancing from AB09ND, balancing from TB01ID, and no balancing.

We found that the only balancing option that gave us a segment of continuous RMS gradient was AB09ND. Both TB01ID and the no balancing showed a scatter which should not be the case.

We have attached the RMS plots for all three situations.

Trivial demonstration of counting statistics

This is mostly a test to see how to use jupyter notebooks for communications. They can't at the moment, but here it is exported as a pdf.

Cleaned the Buzz Repo

I have cleaned up the buzz repo and made sure to update the solvers.py file with the new BH1_solvers_test.py from the old 300m repo. I have rerun the ASC notebooks and verified that the new code still functions properly. I have tagged this version as "cleaned_v1".

I also added pytests in the file T_Test4Lee. These tests will allow for tests to be run on the currently working solver as well as developing a new solver in  the BH1_solvers_test.py file. By setting the solver in the calcOpt function as "test" the solver will use the solver in the file. This can also be done by setting the solver in the test params to "test". Hopefully this allows for easy prototyping of the solver with out interfering with the other solvers or code

Buzz code matching old 300m cavity code

[Ian, Lee]

Using saved versions of the models from the 300m cavity repo (https://git.ligo.org/wieldphysics/ligo300mfiltercavity) we have matched the resulting controllers from the 'ligo300mfiltercavity/T_ASC_mixed_H_BH2.py solver2' test with new buzz code (https://git.ligo.org/ian.macmillan/buzz).

The 300m result shows the mixed H2/Hinf result at one weight for the two FOMs: (BNS FOM: 250000, and the Flat FOM: 1). The multiple traces comes from the gamma parameter being decreased flattening the closed loop gain. These results (with the file prefix "300m") are in the attachments. These controllers match with the open and closed loop gain that we get from the Buzz code also in the attachments with the prefix "buzz".

I also attached two RMS Plots. The First one (with the prefix "RMS_single" is of the single FOM weighting which is the controllers we calculated in the comparison above. As is seen on the plot the phase margin diverges from zero as the gamma decreases. This is what we expect but was not what we were seeing earlier because of a bug. It may be wise not to trust 'control.margin()'.

Once we know that the result of our two codes match I wanted to explore the what other weightings did. The last plot (prefix "RMS_multi") is using a weighting of F1_gain form 250 to 250000 with 4 different weightings, where F2_gain (flat FOM) is 1/F1_gain. The results show that either the solver is very fragile or maybe I haven't picked the correct weighting. It is possible that the weighting is well out of the stable regime for the solver. This would be strange because the max F1 weighting is 250,000 which should be the most unstable weighting combo since the solver needs a non-zero D matrix. This is disappointing but one good thing is that its border seems to follow the nice optimal RMS limiting curve set by the H2 solver.

First acquired lock on the cryo lab west cavity

I successfully locked the cryo west cavity using the laser lock box on the moku yesterday. The main catalyst to this was that the PD being used to measure the REFL signal had a bandwidth of ~10 MHz and was attenuating the 32.7 MHz modulation signal. We ordered some newport 1811 PDs (BW = 125 MHz), and the modulation signal shot up by several orders of magnitude. Note that there is now a lens in front of the REFL PD because the diode on the 1811 is very small, also the damage threshold on these is MUCH LOWER than some of the thorlab equivalents. Don't send > 1mW towards the cavity.

First, the settings of the laser lock box that were used for initial lock can be seen in the attached text file, as well as a screen shot of the lockbox while locked. The process I was using was:

1) Make sure the TEC setpoint is roughly centered to ensure maximum range on the slow loop. Manual engage the slow loop.

2) Slide the slow loop offset until its roughly near the cavity resonance, i.e. you see the large dip in REFL PD.

3) Engage the laser lock box assist function, which is this button. You should now see the REFL PD dip is centered on the error signal zero crossing point, along with some cross-hairs highlighting the zero crossing point on the error signal. These are clickable. Click the zero point that corresponds to the RELF PD dip (sometimes the moku adds additional cross-hairs that are garbage). I'm realizing I don't have a screenshot of this, I'll grab one and comment on this post with it later today.

And thats it! Pretty easy with the moku once everything is set up. I kept the cavity locked for 10+ minutes while tapping the table, the lock seems fairly robust. A minor nuisance, in the other attached photo there seems to be some random low frequency oscillations on the REFL PD that I'm unsure where its coming from. 

Initial test of meeting notes

This is a log entry for meetings. Let's use Section=GQuEST and Primay Task=Meeting for these.