Following this tutorial: Laser Locking With Closed-Loop Transfer Function Measurement (liquidinstruments.com), here's a summary of useful points in measuring the transfer function of the plant, open loop system, etc, which can be useful in the design choices for the laser PID controller (like determining how good the gain parameters are). This was done with just the slow controller enabled. It would be a little more complicated if both slow and fast controllers are enabled because you would have to divide out the fast controller TF (from the Moku configuration, Out A of the LLB would not be the pure error signal). 

Note: there is an error in Figure 1 of the linked tutorial. Noise should be injected AFTER the plant for the subsequent math to be correct. 

Basic idea: To test how good your plant can deal with disturbances, you inject some disturbance and measure the system response. A way to measure these responses is shown here: sys_tf.jpg (we combined the sensing S into the plant P, but the same math applies to the tutorial). Essentially, the math suggests that if we inject disturbances and measure their corresponding output, we can get the open and closed loop transfer function of the system, which informs us about the stability of our controller.

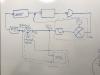
We need to split up the feedback loop into the following components to do this: schematic.jpg. We rigged up the Moku in this configuration to measure all these parameters: Mokuconfig.jpg, using the Laser Lock Box (LLB), Lock In Amplifier (LIA), PID, and Frequency Response Analyzer (FRA). You move the demodulation process into the Lock-In Amplifier (LIA) and perform the injection using a PID as an adder. Then, you use a Frequency Response Analyzer to get the bode plots for the different transfer functions (open loop, plant, etc). In the FRA, you apply a frequency scan to measure the transfer functions. 

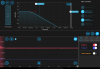
We locked the laser first using the following controller: slowcontroller.png. We measure the open loop transfer function (corrected for the phase going beyond 360 degrees), where we find unity gain (0 dB) occurs at 1.85 Hz with a phase margin of 65 deg: OpenLoopGainTransferFunction.pdf. This means that the system is reasonably stable (a large phase shift is needed to reach instability so the system is robust) and can control below 1.85Hz (can't suppress noise effectively above this).

This open loop TF is given by CP. We can divide CP by the controller transfer function (C) that we applied (dividing the gain and the phase) to get the plant transfer function, which is shown as a Bode plot here: PlantTransferFunction.pdf. A few notes:

• We divided OpenLoopGainTransferFunction.pdf by ControllerTF.pdf (controller bode plot) to get PlantTransferFunction.pdf (plant transfer function). Note that data for the open loop gain TF is not useful beyond ~12 Hz as seen in the noisy signal in the Bode plot (after unwrapping phase). So, we only consider the region of frequencies before 12 Hz in the plant transfer function bode plot.
• To divide the gain, you need to convert both transfer function Bode plots from the log scale of dB to amplitude (20 log (A) = dB) after which you can divide the two plots and reconvert back to dB (otherwise you divide by 0). 
• The plant transfer function is inclusive of the laser and entire demodulation process.
• Thanks Jeff for pointing out that we can figure out the controller based on these two parameters (unity gain frequency and initial magnitude) in the Moku output (slowcontroller.png). This is a first order controller as determined by the number of poles/zeros aka 1. Because there is one corner frequency from the Bode plot, we have G(s) = k / (1+Ts). The math is here (note: omega is in rad/s): math.png. So, our controller C(s) = G(s) = 25.4097/(1+1.14056s). I forgot to take a measure of the controller's phase plot so depending on the sign of -s or +s the controller phase plot is different. Anyways, this is the Bode plot of the controller we used to lock: ControllerTF.pdf. It matches the Moku controller Bode plot (slowcontroller.png). 
• Ian mentioned that the Moku's PID controller displayed is sometimes not reflective of the actual controller because the Moku has limits to its ability to implement the controller so we would use Jeff's code to correct the controller and get the right transfer function bode plot (I think). 

Knowing the plant TF, you can use these functions to find potential resonant peaks or bandwidth limits in the system. This is useful because you want to make sure your controller won't start to amplify those peaks and drive the system out of stable lock. The plant transfer function bode plot has a generally flat magnitude, which is expected because it should not be amplifying any particular frequency. The slight bump at ~4 Hz may be some slight resonance in the system, it shows up in the final noise spectrum as well interestingly enough (NoiseSpectra.pdf), although this is with the slow and fast controller. Ideally, you want the range of your open loop phase margin to be between -90 and 90 degrees for as large of a controller bandwidth as possible. We would be able to model the system fully if we could sum the noise spectra (inside closed loop) and plant transfer function. 

We can also check the goodness of our controller by looking at the disturbance rejection, which is the response put on a disturbance going through the system. You would want the bode plot of the disturbance rejection to be at low magnitude (e.g. negative dB) to suppress the disturbance. To ensure that the perturbations are suppressed enough and you can hold the lock with less noise, the magnitude of the disturbance rejection should not increase beyond 0 dB after the unity gain frequency because then, noise will be amplified in the system (i.e. (1/(1+CP))*N = disturbance rejection TF * Noise --> increased noise in the output). I don't really understand the last sentence of this article where the low frequency gain of the open loop TF matching the disturbance rejection magnitude suggests there is adequate noise suppression: I would think that as long as the magnitude of 1/(1+CP) is small, the magnitude of CP should not matter.