First acquired lock on the cryo lab west cavity

I successfully locked the cryo west cavity using the laser lock box on the moku yesterday. The main catalyst to this was that the PD being used to measure the REFL signal had a bandwidth of ~10 MHz and was attenuating the 32.7 MHz modulation signal. We ordered some newport 1811 PDs (BW = 125 MHz), and the modulation signal shot up by several orders of magnitude. Note that there is now a lens in front of the REFL PD because the diode on the 1811 is very small, also the damage threshold on these is MUCH LOWER than some of the thorlab equivalents. Don't send > 1mW towards the cavity.

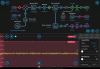
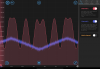
First, the settings of the laser lock box that were used for initial lock can be seen in the attached text file, as well as a screen shot of the lockbox while locked. The process I was using was:

1) Make sure the TEC setpoint is roughly centered to ensure maximum range on the slow loop. Manual engage the slow loop.

2) Slide the slow loop offset until its roughly near the cavity resonance, i.e. you see the large dip in REFL PD.

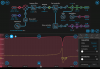
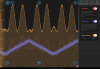
3) Engage the laser lock box assist function, which is this button. You should now see the REFL PD dip is centered on the error signal zero crossing point, along with some cross-hairs highlighting the zero crossing point on the error signal. These are clickable. Click the zero point that corresponds to the RELF PD dip (sometimes the moku adds additional cross-hairs that are garbage). I'm realizing I don't have a screenshot of this, I'll grab one and comment on this post with it later today.

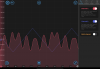
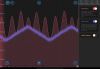
And thats it! Pretty easy with the moku once everything is set up. I kept the cavity locked for 10+ minutes while tapping the table, the lock seems fairly robust. A minor nuisance, in the other attached photo there seems to be some random low frequency oscillations on the REFL PD that I'm unsure where its coming from. 

Initial test of meeting notes

This is a log entry for meetings. Let's use Section=GQuEST and Primay Task=Meeting for these.

LSC Model Not Playing Nice with Mixed H2/Hinf solver

I tried the LSC model (tried attaching but does not accept .mat files) with the H2 solver And it worked like normally. You can see these results in the "LSC_H2_Results.pdf" attachment.

When trying the LSC model with the H2/Hinf Mixed solver it struggled to recover even the H2 results. This is with a gamma going from 1e3 down to 1e-1 (not igsq). On the H2 result it looks like the Closed loop is peaking at about 100 so this should be plenty to at least recover the H2 results. but I am left with the results seen in "LSC_H2HinfMix_Results.pdf"

It is possible that this is a problem with the Zinf connection but I will have to investigate further. I also still need to try the damping loop. Also I got multiple color bars working using This.

Paper Plots for H2/Hinf Optimal Controls Paper

Here I make a list of all of the plots that I want to include in the final $H_2$/$H_{inf}$ Optimal Controls paper. The paper should look at 3 models: - The damping loop - The LSC - The ASC For each of these models should have a few plots: 1) Open Loop Plot: This plot should show the open loop transfer function of the full system. It should show the current loop as well as a number of different loops for varying FOM weight and varying $H_{inf}$ upper limit {gamma} 2) An RMS Plot: This will show the $H_2$ norm (RMS output) from the white noise inputs to the FOM outputs. This plot will be a scatter plot with one FOM being the BNS FOM and one being the flat FOM 3) Closed Loop Plot: Although this may not make it into the paper I need to make a closed loop plot that shows the closed loop transfer function for the current controller and the controllers calculated for decreasing $H_{inf}$ upper limit {gamma}. This plot will show the mixed controller is limiting the peak of the closed loop magnitude. 4) A Noise Plot: this plot will characterize the plant model for the given models above it will include the magnitude of the noise blocks. In addition to all those plots I will want to create some general plots that are one off: 1) I will want to create a FOM plot which shows the Flat FOM the BNS FOM and the simplified BNS FOM that is used. Only Magnitude will be necessary

Frequency noise measurement

Remeasured the frequency noise with the 785 after the visibility improvement. Assuming my calibration to Hz/sqrt(hz) is correct, the measurement is still yielding several orders of magnitude larger than what rio claims it to be. Investigating this today.

 

For reference, the SR785 measures a quantity is V/sqrt(Hz). To convert to frequency noise I do S / (L/c * B*2*pi) where S is the measurement, L is the path length difference between the two arms and B is the fringe amplitude. V/sqrt(Hz) / (m/(m/s) * V) = Hz/sqrt(Hz).

Laser Frequency Characterization with Mokus

Lee came into the lab today and discovered that the TEC controller's range on the integrator is very small, which is why I was having trouble driving the laser frequency. If you center on this range (~10.2 kOhm) you can then drive a signal into the back of the TEC so that there are constant fringes on the Mach-Zehnder read out. I did this via the moku (15 mV @ .1 Hz, corresponds to roughly 1 fringe). "2.png" is this first attempt, red is the readout PD, blue is the driving signal. "3.png" is then hooking up a PD farther upstream to use as a power reference instead of the driving signal (see also cryolab_frequency_noise_measurement_pdf.pdf, the lighter color laser path in that is used). "4.png" is then using the moku's math channels to do (readout PD)/(power reference) to give the fringes at a constant offset. At this point its very easy to align to maximize these fringes. "7.png" shows the improved visibility. "5.png" shows the moku set up used. There are some shenanigans with the input ranges when using an oscilloscope in multi-instrument mode where you either have it on 400mV setting and its saturated, or its on 4V setting and it auto attenuates the signal by 20dB. So the digital filter box is undoing that 20dB attenuation. For unequal powers, I believe the formula is V =(2*sqrt(34*99)/(99+34))=87%, so not perfect but a vast improvement.

Hello World!

According to all known laws of aviation, there is no way a bee should be able to fly. Its wings are too small to get its fat little body off the ground. The bee, of course, flies anyway because bees don't care what humans think is impossible. Yellow, black. Yellow, black. Yellow, black. Yellow, black. Ooh, black and yellow! Let's shake it up a little. Barry! Breakfast is ready! Coming! Hang on a second. Hello? Barry? Adam? Can you believe this is happening? I can't. I'll pick you up. Looking sharp. Use the stairs, Your father paid good money for those. Sorry. I'm excited. Here's the graduate. We're very proud of you, son. A perfect report card, all B's. Very proud. Ma! I got a thing going here. You got lint on your fuzz. Ow! That's me! Wave to us! We'll be in row 118,000. Bye! Barry, I told you, stop flying in the house! Hey, Adam. Hey, Barry. Is that fuzz gel? A little. Special day, graduation. Never thought I'd make it. Three days grade school, three days high school. Those were awkward. Three days college. I'm glad I took a day and hitchhiked around The Hive. You did come back different. Hi, Barry. Artie, growing a mustache? Looks good. Hear about Frankie? Yeah. link [test](google.com)

The OSLogbook

Welcome to the OSLogbook application.